Ecuaciones cuadráticas

Una ecuación de segundo grado1 2 o ecuación cuadrática de una variable es una ecuación que tiene la forma de una suma algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por unpolinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es:




donde x representa la variable y a, b y c son constantes; a es un coeficientecuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede representar mediante una gráfica de una función cuadrática oparábola. Esta representación gráfica es útil, porque la intersección de esta gráfica con el eje horizontal coinciden con las soluciones de la ecuación (y dado que pueden existir dos, una o ninguna intersección, esos pueden ser los números de soluciones de la ecuación).
Historia
El origen y la solución de las ecuaciones de segundo grado son de gran antigüedad. En Babilonia se conocieron algoritmos para resolverla. El resultado también fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de ecuaciones (aunque su método sólo proporcionaba una de las soluciones, aun en el caso de que las dos soluciones sean positivas). También el matemático judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la solución de estas ecuaciones.
Fórmula cuadrática
Para una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas (si los coeficientes son reales y existen dos soluciones no reales, entonces deben ser complejas conjugadas). Se denomina fórmula cuadrática3 a la ecuación que proporciona las raíces de la ecuación cuadrática:


donde el símbolo ± indica que los valores
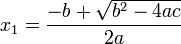y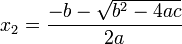
constituyen las dos soluciones.
Discriminante

Ejemplo del signo del discriminante:
■ < 0: no posee soluciones reales;
■ = 0: posee una solución real (multiplicidad 2);
■ > 0: posee dos soluciones reales distintas.
En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre dediscriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con el símbolo Δ (delta):
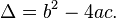
Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real de multiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.
Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje de las abscisas: X):.
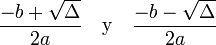Una solución real doble si el discriminante es cero (la parábola sólo toca en un punto al eje de las abscisas: X):
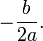
Dos números complejos conjugados si el discriminante es negativo (la parábola no corta al eje de las abscisas: X):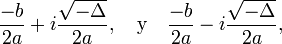donde i es la unidad imaginaria.
En conclusión, las raíces son distintas si el discriminante es no nulo, y son números reales si –sólo si– el discriminante es no negativo.
Ecuación bicuadrática
Éstas son un caso particular de la ecuación de cuarto grado. Les faltan los términos a la tercera y a la primera potencia. Su forma polinómica es:
Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable
Con lo que nos queda: El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula:
Ahora bien, esto no nos da las cuatro soluciones esperadas. Aún hemos de deshacer el cambio de variable. Así las cuatro soluciones serán:

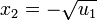
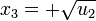
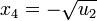
Ecuaciones cuadráticas (Vídeo)

                                          


                                              Presentación de ecuaciones cuadráticas
                                                                         
                                     http://www.slideshare.net/lacienciamatematica/01-ecuaciones-cuadrticas














                                                Mapa mental de ecuaciones cuadráticas


                                                                       

                                                                          Coclusión:

Este tema fue el mas complicado para mi ya que en segundo grado no aprendi nada en mate pues no teníamos profe, pero aun asi sabia interpretarlas bueno solo las ecuaciones de primer grado ya que en las otras se me complicaba, para mi lo mas difícil no fue resolverlas si no encontrar las ecuaciones, se me dificultaban eso problemas donde teníamos que encontrar la ecuación correspondiente para solucionar el problema, pero a fin de cuentas ya puedo dominarlo un poquito mas, espero poder aprender mas de este tema que es complicado para mi.