Estadística y probabilidad:
La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos
por las observaciones, para poder hacer comparaciones y sacar conclusiones.
Un estudio estadístico consta de las siguientes fases:
Recogida de datos.
Organización y representación de datos.
Análisis de datos.
Obtención de conclusiones.
La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.
Son los experimentos de los que podemos predecir el resultado antes de que se realicen.
Ejemplo:
Si dejamos caer una piedra desde una ventana sabemos, sin lugar a dudas, que la piedra bajará. Si la arrojamos hacia arriba, sabemos que subirá durante un determinado intervalo de tiempo; pero después bajará
Son aquellos en los que no se puede predecir el resultado, ya que éste depende del azar.
Si lanzamos una moneda no sabemos de antemano si saldrá cara o cruz
Si lanzamos un dado tampoco podemos determinar el resultado que vamos a obtener.
La teoría de probabilidades se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro. Con este fin, introduciremos algunas definiciones:
Suceso
Es cada uno de los resultados posibles de una experiencia aleatoria.
Al lanzar una moneda salga cara.
Al lanzar una moneda se obtenga 4.
Espacio muestral
Es el conjunto de todos los posibles resultados de una experiencia aleatoria, lo representaremos por E (o bien por la letra griega Ω).
Espacio muestral de una moneda:
E = {C, X}.
Espacio muestral de un dado:
E = {1, 2, 3, 4, 5, 6}.
Suceso aleatorio
Suceso aleatorio es cualquier subconjunto del espacio muestral.
Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:
1. El espacio muestral.
E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}
2. El suceso A = {extraer tres bolas del mismo color}.
A = {(b,b,b); (n, n,n)}
3. El suceso B = {extraer al menos una bola blanca}.
B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}
4. El suceso C = {extraer una sola bola negra}.
C = {(b,b,n); (b,n,b); (n,b,b)}
Aquí le tengo una presentación de Power point del tema:
Aquí les tengo un vídeo del tema:
Mi conclusión del tema es:
Yo opino que este tema es muy interesante, ya que nos habla de las probabilidades que puede tener por ejemplo: un dado al lanzarlo al aire no sabemos que número va a caer pero de antemano sabemos cuales son los posibles resultados que puede tener; 1,2,3,4,5,6. :)
Binomio al cuadrado:
Binomio de suma al cuadrado
Un binomio al cuadrado (suma) es igual es igual al cuadrado del primer término, más el doble producto del primero por el segundomás el cuadrado segundo.
(a + b)2 = a2 + 2 · a · b + b2
(x + 3)2 = x 2 + 2 · x ·3 + 3 2 = x 2 + 6 x + 9
Binomio de resta al cuadrado
Un binomio al cuadrado (resta) es igual es igual al cuadrado del primer término, menos el doble producto del primero por el segundo, más el cuadrado segundo.
(a − b)2 = a2 − 2 · a · b + b2
(2x − 3)2 = (2x)2 − 2 · 2x · 3 + 3 2 = 4x2 − 12 x + 9
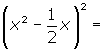
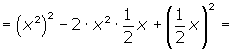
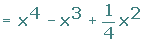
El desarrollo de un un binomio al cuadrado se llama trinomio cuadrado perfecto.
a2 + 2 a b + b2 = (a + b)2
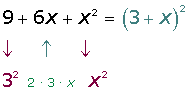
a2 − 2 a b + b2 = (a − b)2
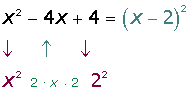
Aquí les tengo un vídeo del tema:
Esta es una presentación en Power point del tema:
Mi conclusión del tema es:
Mi opinión de este tema es que un binomio al cuadrado (suma) es igual es igual al cuadrado del primer término, más el doble producto del primero por el segundo más el cuadrado segundo. :)
Factor común:
Para comenzar, comparemos las multiplicaciones con los factores y veamos si podemos descubrir un patrón.

Usan la propiedad distributiva. Cuando multiplicamos, tenemos que:  . Cuando factorizamos
. Cuando factorizamos  .
.
Para factorizar un binomio, debemos hallar un factor (en este caso a) que sea común a todos los términos. El primer paso para tener una expresión completamente factorizada es seleccionar el máximo factor común,  . Aquí tenemos como hacerlo:
. Aquí tenemos como hacerlo:
Máximo factor común (MFC).- El término  , es el MFC de un polinomio sí:
, es el MFC de un polinomio sí:
- a es el máximo entero que divide cada uno de los coeficientes del polinomio, y
- n es el mínimo exponente de x en todos los términos del polinomio.
De este modo para factorizar  , podríamos escribir
, podríamos escribir 
Pero no está factorizado por completo por que  puede factorizarse aún más. Aquí el mayor entero que divide a 16 y 8 es 6, y el mínimo exponente de x en todos los términos es
puede factorizarse aún más. Aquí el mayor entero que divide a 16 y 8 es 6, y el mínimo exponente de x en todos los términos es  . De esta manera la factorización completa es
. De esta manera la factorización completa es  . Donde
. Donde  es el MFC.
es el MFC.
EJEMPLO:
Factorizar 
EJEMPLO:
Factorizar 
EJEMPLO:
Factorizar 

EJEMPLO:
Factorizar 

EJEMPLO:
Factorizar 

EJEMPLO:
Factorizar 

EJEMPLO:
Factorizar 

Aquí les tengo una presentación de power point del tema:
Este es un vídeo del tema:
Mi conclusión del tema es:
Para mí este tema se me hizo un poco complicado ya que teníamos que resolver los problemas haciendo una tabla con la cual determinaríamos cuál es el ''máximo común divisor'' osea el número que pueda dividir a todos los términos, después de eso teníamos que dividir todos los términos con el número osea el ''máximo común divisor'' :)
Trinomio cuadrado perfecto:
Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.
En el trinomio cuadrado perfecto los términos cuadrados son siempre positivos, en cambio el término del doble producto puede ser negativo; en este caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el trinomio dado, del ejemplo anterior tenemos:

Ambas son respuestas aceptables.
Regla para conocer si un trinomio es cuadrado perfecto.
Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos (o tienen raíz cuadrada exacta) y son positivos y el segundo termino es el doble producto de sus raíces cuadradas.
Ejemplos:

Aquí les tengo una presentación de power point del tema:
Este es un vídeo del tema:
Mi conclusión del tema es:
Este tema está un poco complicado, primero tenemos la ecuación de 3 términos a esa ecuación le tenemos que sacar la raíz cuadrada a los dos que estén de lado izquierdo o derecho y multiplicar la raíz cuadrada por 2 para obtener como resultado el segundo término y después factorizar para tener la ecuación del principio.
Este tema está un poco complicado, primero tenemos la ecuación de 3 términos a esa ecuación le tenemos que sacar la raíz cuadrada a los dos que estén de lado izquierdo o derecho y multiplicar la raíz cuadrada por 2 para obtener como resultado el segundo término y después factorizar para tener la ecuación del principio.
Trinomio de segundo grado:
Dada una ecuación de seguno grado completa:
ax2 + bx + c = 0
Se puede descomponer en factores como sigue:
a · (x - x1) · (x - x2) = 0
Aquí les tengo una presentación de power point:
Aquí les tengo un vídeo del tema:
Mi conclusión del tema es:
Para este tema se tenía que descomponer en factores el trinomio de segundo grado, por ejemplo: P(x) = ax2 + bx + c, se iguala a cero y se resuelve la ecuación de 2º grado. Si las soluciones a la ecuación son x1 y x2, el polinomio descompuesto será:
a x2 + bx +c = a · (x -x1 ) · (x -x2 ).
Diferencia de cuadrados:



a x2 + bx +c = a · (x -x1 ) · (x -x2 ).
Diferencia de cuadrados:
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Al estudiar los productos notables teníamos que:

En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:

Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Pasos:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).
Ejemplo explicativo:

Aquí les presento un vídeo del tema:
Esta es una presentación en power point del tema:
Mi conclusión del tema es:
Este tema es un poco fácil, ya que sólo se tiene que sacar la raíz cuadrada exacta de los términos de la ecuación que son dos y el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario. :)
Este tema es un poco fácil, ya que sólo se tiene que sacar la raíz cuadrada exacta de los términos de la ecuación que son dos y el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario. :)
Resolución de ecuaciones por factorización:
Una Forma de resolver ecuaciones cuadráticas consiste en factorizar las expresiones algebraicas. Por ejemplo, la ecuación:x2+7x+10=18
Se puede resolvar factorizando el trinomio x2+7x+10; la ecuación queda así:
(x+5) (x+2)=18
Una manera de resolver esta ecuación factorizada consiste en buscar parejas de números que multiplicados den 18 y que uno de ellos sea tres unidades menor que el otro.
En este caso, hay dos parejas de números que cumplen estas dos condiciones:
(3) (6) = 18
(-3) (-6) = 18
Entonces, se tiene que: (x+5) (x+2)=18
(3) (6) = 18
Donde x=1, porque x+2 = 1+2 = 3 y, x+5 = 1+5 = 6
Además se tiene que: (x+5) (x+2)=18
(-3) (-6) = 18
Donde x = -8, porque x+2 = -8+2 = -6 y, x+5 = -8+5 = -3
NOTA: Si el producto de dos números es igual a cero, al menos uno de ellos tiene que ser igual a cero.
Una ecuación cuadrática factorizada e igualada a cero se resuleve al encontrar los números que hacen valer cero a los factores. Por ejemplo, la ecuación cuadrática factorizada:
(x-7) (x+11)=0
Se soluciona al encontrar los vlaores de x que hacen valer cero a los factores, es decir:
x-7 = 0 y x+11 = 0
Donde se obtiene: x1 = 7 y x2 = -11
Entonces 7 y -11 son soluciones porque al sustituirlos en la ecuación y efectuar las operaciones, se obtiene 0.
Sustituyendo 7: (7-7)(7+11) = (0) (18) = 0
Sustituyendo -11: (-11-7)(-11+11) = (-18) (0) = 0
Para resolver una ecuación cuadrática usando la factorización es conveniente pasarla primero a su forma general.
Por ejemplo, la ecuación x2-3x-5 = 35 se puede resolver de la siguiente manera:
Se pasa la ecuación a su forma general: x2-3x-40 = 0
Se factoriza: (x-8) (x+5) = -5
Se encuentran los valores de x que hacen cero los factores: x1 = 8 y x2 = -5
Se verifican las soluciones sustituyenddo en la ecuación original:
Para x1 = 8 (8)2-3(8)-5 = 64-24-5 = 35
Para x2 = -5 (-5)2-3(-5)-5 = 25+15-5 = 35
Aquí les presento un vídeo del tema:
Les presento una presentación en power point del tema:
http://www.authorstream.com/Presentation/ivasanpi-1882367-ecuaciones-de-segundo-grado-por-factorizacion/
Mi conclusión del tema es:
Este tema estuvo medio difícil porque a los términos teníamos que encontrar de que caso de factorización se trataba, después factorizar los términos, ya que tenemos eso, igualar cada término a (0) como consiguiente comprobar cada término para verificar que estaba bien la igualación y la solución será los términos correctos.






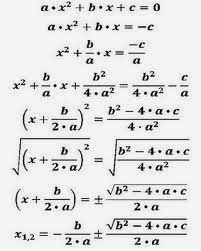


 , siendo
, siendo  cualquier error e y
cualquier error e y  su probabilidad, y expuso tres propiedades de esta curva:
su probabilidad, y expuso tres propiedades de esta curva: igual a 0;
igual a 0;
 y
y  constantes que dependen de la precisión de la observación. Expuso dos demostraciones, siendo la segunda esencialmente la misma de
constantes que dependen de la precisión de la observación. Expuso dos demostraciones, siendo la segunda esencialmente la misma de  , el error probable de una única observación, es bien conocida.
, el error probable de una única observación, es bien conocida.
 ) que sólo la descripción estadística de sus propiedades es viable.
) que sólo la descripción estadística de sus propiedades es viable.
